
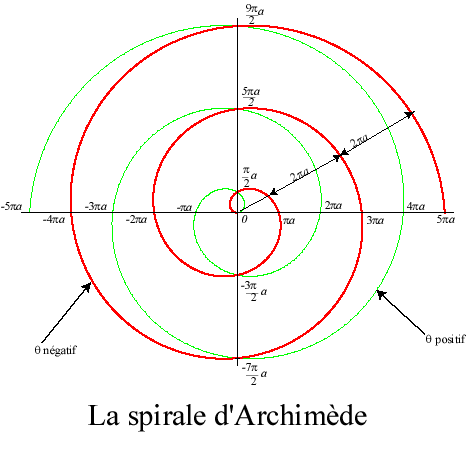
Set_Draw_Colour (( 0, 220, 0, 255 )) Draw_Archimedean_Spiral Window. Using Archimedes screws as water pumps (Archimedes screw pump (ASP) or screw pump) dates back many centuries. In other words, the spiral consists of all. The Archimedes screw, also known as the Archimedean screw, hydrodynamic screw, water screw or Egyptian screw, is one of the earliest hydraulic machines. Fill ( Rectangle => ( 0, 0, Width, Height )) Renderer. In polar coordinates the Archimedean spiral above is described by an equation that couldnt be simpler: rtheta. Set_Draw_Colour (( 0, 0, 0, 255 )) Renderer. Buy Math Art Prints-Archimedean Spiral, Eulers Formula, Fibonacci Golden Spiral, Pythagoras Theorem-Set of Four Gallery Wall 8x10 Unframed - Gift & Decor. Positive_Sizes '( Width, Height ), Flags => 0 ) SDL. It has been used to trisect angles and to square the circle. Natural_Coordinates '( X => 10, Y => 10 ), Size => SDL. It was discovered by Archimedes in about 225 BC in a work On Spirals. Create ( Win => Window, Title => "Archimedean spiral", Position => SDL. Quit then return end if end loop end loop end Wait begin if not SDL. int ( R * Sin ( T, 2.0 * Pi )))) exit when T >= T_Last T := T + Step end loop end Draw_Archimedean_Spiral procedure Wait is use type SDL. int ( R * Cos ( T, 2.0 * Pi )), Y => Height / 2 - SDL. Pi Step : constant := 0.002 T : Float R : Float begin T := T_First loop R := A + B * T Renderer. In the Archimedean spiral or linear spiral (Figure 1, middle), it is the spacing between intersections along a ray from the origin that is constant.
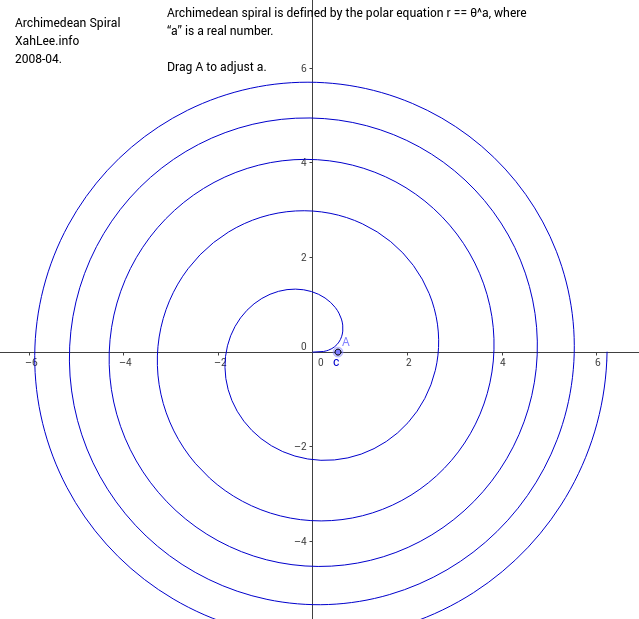
The function is in polar coordinates or in this implementation, in rectangular coordinates. The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes.It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Rotating this with uniform angular velocity about its centre will result in uniform linear motion of the point where it crosses the y y y-axis. I start with the printout of the Archimedean Spiral Antenna. Log-Periodic Spiral Antenna, a 0.2, Approximately 2.5 Turns. Events procedure Draw_Archimedean_Spiral is use type SDL. This Demonstration uses parametric equations and radius vectors to plot Archimedess spiral (blue) and the curve of its tangents (orange), which represent the derivative. First, here are some Spiral Antenna Patterns you can print out if you want to create your own spiral antennas: Archimedean Spiral, a 0.22, Approximately 3.2 Turns. With _Functions with with with procedure Archimedean_Spiral is Width : constant := 800 Height : constant := 800 A : constant := 4.2 B : constant := 3.2 T_First : constant := 4.0 T_Last : constant := 100.0 Window : SDL. Therefore a simple implementation for Sin and Cos function has been provided. The below example generates points along the spiral continuously, relative to the maxSteps value.Action! does not provide trigonometric functions. As it said in Archimedean spiral, it can be described by the equation r a + b and the constant separation distance is equal to 2b if we measure in radians. Then it’s a matter of deciding how many points to generate on the curve, and the angle between the points. Substituting in, r=a+bθ, we get: x = (a + bθ) * cos θ The formula’s for doing this are:: x = r * cos θ According to the software that i am using r, a, n, b, th and Th values are correct. But the problem arises with the output values x and y. So how do we create the spiral? Well really it’s all about converting the polar coordinates to cartesian coordinates. The output which i am getting is an Archimedean Spiral, thats fine. There are two different forms of spiral, that coil in opposite directions – one when θ>0, the other when θ<0. The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. Here a turns the spiral, while b controls the distance between successive turnings. The equation for the Archimedes spiral can be expressed in polar coordinates, ( r=length, θ=angle), i.e. Things that humans create tend to follow the Archimedes spiral – a coil of clay, cinnamon rolls, Swiss rolls, paper towels, gramophone records – basically anything that gets rolled up. The Archimedean spiral is the trajectory of a point moving uniformly on a straight line of a plane, this line turning itself uniformly around one of its points. The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes.


 0 kommentar(er)
0 kommentar(er)
